Метод выделения полного квадрата. Вывод формулы корней полного квадратного уравнения.

При решении задач разного рода часто можно столкнуться с квадратными, биквадратными и т.д. уравнениями. Конечно, для решения квадратных и всех к ним сводящихся требуется уметь решать сами квадратные уравнения. Это можно делать многими способами (теорема Виета, устные способы решения и быстрой оценки корней рассматривается на отдельной странице, ещё неполные квадратные уравнения решаются не так как полные - проще).

Метод выделения полного квадрата

Итак, традиционно корни многочлена находят, разложив его на множители. Разложение на множители очень помогает в поиске корней, так как, если произведение равно нулю, то один из множителей равен 0. При разложении на множители помогает вынесение общего множителя за скобку (пожалуй, это первое, что следует делать при разложении на множители). Далее обычно происходит группировка (если нет общего множителя, или этого не достаточно). Это по аналогии можно назвать методом группировки: одночлены разделяются по группам, имеющим общий множитель. Далее в идеале появляется общий множитель у всего выражения, который можно вынести и продолжить разложение. Потом, используя формулы сокращённого умножения, можно закончить разложение.

Однако, есть ещё один приём, заслуживающий отдельного внимания, основанный на формулах квадрата суммы и разности. Метод выделения полного квадрата. Особенность этих формул в том, что в них есть квадраты двух выражений и их удвоенное произведение. Если найти что-то, отдалённо напоминающее квадрат суммы или разности, но без какой-то необходимой части, то её можно прибавить, а затем отнять, тем самым не меняя конечного значения выражения. Далее, свернув квадрат суммы/разности, обычно нужно применить ещё какую-то формулу (например, разности квадратов) или совершить какую-то последовательность действий, и многочлен разложится на множители.

Пример разложения на множители методом выделения полного квадрата:

y^{4} + 4 x^{4} = {(y^{2})}^{2} + 2^{2} {(x^{2})}^{2} + 2 \times 2 x^{2} y^{2} - 2 \times 2 x^{2} y^{2} = {(y^{2} + 2 x^{2})}^{2} - 4 x^{2} y^{2} = (y^{2} + 2 x^{2} - 2 x y) (y^{2} + 2 x^{2} + 2 x y)

Метод выделения полного квадрата имеет много применений, связанных с квадратными уравнениями. Его можно применить к квадратному трёхчлену (общему виду квадратного уравнения).

a x^{2} + b x + c = a (x^{2} + \frac{b}{a} \times x + \frac{c}{a}) = a (x^{2} + \frac{b 2}{a 2} x + \frac{c}{a}) = a (x^{2} + 2 \frac{b}{2 a} + \frac{c}{a}); метод выделения полного квадрата : a x^{2} + b x + c = a ([x^{2} + 2 \frac{b}{2 a} + \frac{b^{2}}{4 a^{2}}] - \frac{b^{2}}{4 a^{2}} + \frac{c}{a}) = a [{(x + \frac{b}{2 a})}^{2} - \frac{b^{2}}{4 a^{2}} + \frac{c}{a}] = a {(x + \frac{b}{2 a})}^{2} - \frac{b^{2} - 4 a c}{4 a}

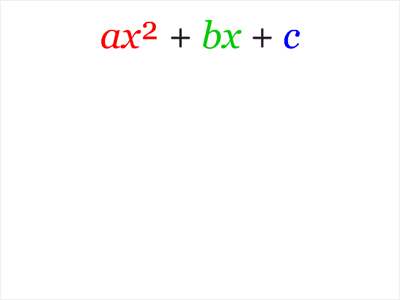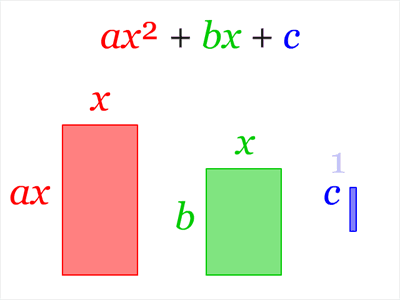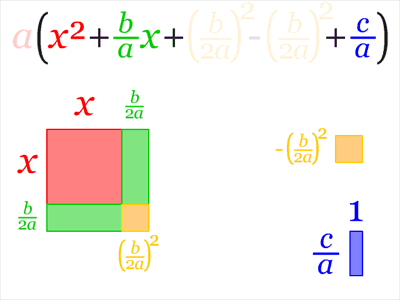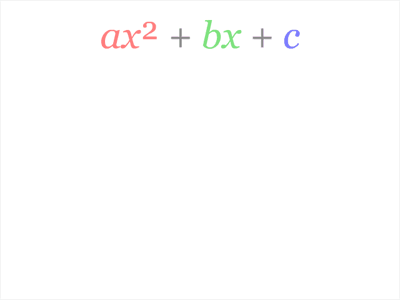
Анимированная иллюстрация к методу выделения полного квадрата — Великолепная иллюстрация к методу выделения полного квадрата из Wikimedia Commons

О свойствах и некоторых полезных следствиях получившегося представления можно прочитать здесь. Это ещё одна удобная форма представления квадратичной функции.

Также метод выделения полного квадрата позволяет именно решать квадратные уравнения. Для этого есть хорошо определённый и вполне известный алгоритм (написан для ax²+bx+c = 0).

Разделить каждую часть на a - старший коэффициент (при квадрате).
Вычесть из обеих частей свободный член c/a.
Добавить с обеих сторон квадрат половины среднего коэффициента b/a (при x).
Свернуть левую часть и упростить правую (если нужно).
Произвести два линейных уравнения, приравнивая квадратный корень левой части к положительному и отрицательному квадратному корню правой.
Решить получившуюся систему.

У многих квадратных уравнений есть более красивые и простые решения.

Пример нестандартного, но более интуитивного и быстрого решения:

\begin{matrix} x^{2} + 14 x + 45 = 0 \\ x^{2} + 14 x + 45 + 4 - 4 = 0 \\ (x^{2} + 14 x + 49) - 4 = 0 \\ {(x + 7)}^{2} - 4 = 0 \\ {(x + 7)}^{2} - 2^{2} = 0 \\ (x + 7 - 2) (x + 7 + 2) = 0 \\ (x + 5) (x + 9) = 0 \\ [\begin{matrix} x + 5 = 0 \\ x + 9 = 0 \end{matrix}  \\ [\begin{matrix} x = - 5 \\ x = - 9 \end{matrix}  \\ Ответ: x \in \{-5; -9\} . \end{matrix}

Пример решения уравнения с использованием алгоритма:

\begin{matrix} 4 x^{2} + 20 x - 24 = 0 | \times \frac{1}{4} \\ x^{2} + 5 x - 6 = 0 | - (- 6) \\ x^{2} + 5 x = 6 | + {2.5}^{2} \\ x^{2} + 5 x + 6.25 = 12.25 \\ {(x + 2.5)}^{2} = 12.25 \\ [\begin{matrix} x + 2.5 = 3.5 \\ x + 2.5 = - 3.5 \end{matrix}  \\ [\begin{matrix} x = 1 \\ x = - 6 \end{matrix}  \\ Ответ: x \in \{1; - 6\} . \end{matrix}

Формула корней полного квадратного уравнения

Формула корней квадратного уравнения из Wikimedia Commons

Решение квадратных уравнений с разложением на множители - это достаточно хороший способ решения. Однако, он далеко не единственный. Корни квадратного уравнения также можно вычислять по формуле (используя их зависимость от дискриминанта и коэффициентов - подробнее о дискриминанте и зависимости), но данная формула также выводится, используя описанный выше метод выделения полного квадрата (хотя, как и везде, точное следование заданному алгоритму необязательно, и есть другие (возможно более удобные) пути выведения формулы).

Начнём, как водится, с записи квадратного уравнения общего вида: ax²+bx+c = 0. А затем, можно проделать над уравнением ряд действий, основанных на алгоритме.

\begin{matrix} a x^{2} + b x + c = 0 | \times \frac{1}{a} \\ x^{2} + \frac{b}{a} x + \frac{с}{a} = 0 \\ {(x + \frac{b}{2 a})}^{2} = \frac{b^{2}}{4 a^{2}} - \frac{c}{a} \\ {(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}} \end{matrix}

Выражение b² - 4ac называется дискриминантом квадратного уравнения (подробнее о дискриминанте можно прочитать по ссылке выше). Его можно обозначать D.
Получается.

[\begin{matrix} x + \frac{b}{2 a} = \sqrt{\frac{D}{4 a^{2}}} \\ x + \frac{b}{2 a} = - \sqrt{\frac{D}{4 a^{2}}} \end{matrix}

Используя свойство квадратного корня из дроби, получаем конечную формулу корней квадратного уравнения.

[\begin{matrix} x_{1} = \frac{- b + \sqrt{D}}{2 a} \\ x_{2} = \frac{- b - \sqrt{D}}{2 a} \end{matrix}

Это называется основной формулой корней квадратного уравнения. Далее следовало бы обсудить как по дискриминанту определить вид корней и т.д., но это тоже описано по ссылке выше.

Соответственно при решении квадратных уравнений по формуле целесообразно поступать по данному алгоритму.

Вычислить дискриминант.
Сравнить дискриминант с нулём.
Найти корни по формуле.
Если дискриминант меньше 0, то уравнение не имеет корней в поле действительных чисел $ℝ$ .